(2007-Primer día, Problema 6)

Solución

El polinomio puede tener 0 coeficientes no nulos, ya que  cumple que , para todo número complejo  de longitud unidad.

Si tiene algún coeficiente no nulo, podemos expresar  como

, con , donde  es el número de coeficientes no nulos que queremos hallar, 

Podemos suponer sin pérdida de generalidad que , ya que si para un determinado  existe un polinomio  que cumple que  para todo  con , con , entonces tenemos que el polinomio

, cumple que  para todo  con , teniendo este polinomio 0 como exponente del último término.

Tenemos entonces que . Los  con  son de la forma , con , luego en ellos se cumple que

Por tanto,

Luego hay que ver los valores de  para los que existe un polinomio cumpliendo las condiciones del enunciado, y con  para todo :

Si  para todo , entonces  (se puede poner el menor estricto, porque  es una función continua no constante).

Tenemos por tanto que

Entonces  por lo que, al ser , necesariamente se ha de cumplir que  y 

Vemos que  puede ser 1 ó 2: El polinomio  cumple que  para todo  con , y el polinomio  cumple que  para todo  con .

Vemos por último que  no puede ser 3, por lo que los únicos valores posibles son .

Para , podemos llamar , y , siendo el grado del polinomio entonces .

Para ver que ningún polinomio con tres coeficientes que sean  cumple la condición del enunciado, vemos primero que basta con demostrarlo para polinomios que tengan más coeficientes 1 que : Si para todo polinomio  con tres coeficientes que sean  y con más coeficientes 1 que se cumple que existe un  con  y tal que , si tomamos un polinomio  con tres coeficientes que sean  y con más coeficientes  que 1, tenemos que , teniendo  más coeficientes 1 que , por lo que existe un  con  y tal que , y entonces .

De entre los polinomios con 2 coeficientes 1 y un coeficiente  nos podemos quedar con los de la forma  y , ya que si para todos los polinomios de esta forma existe un  con  y tal que , para un polinomio  existirá  con 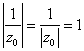 que cumple que

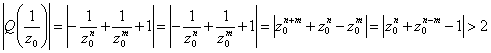, ya que el último polinomio es de tipo , en vez de con  con . Por tanto, basta con considerar los polinomios ,  y .

Para los primeros, existe  con  tal que , luego no cumplen la condición del enunciado.

Para los segundos polinomios, tenemos que, si , con  par, entonces  cumple que

Entonces, se cumple que .

Como , tenemos que , y como , tenemos que , al ser , luego , y , por lo que .

Si , con  impar, entonces  cumple que .

Entonces, se cumple que .

Como , tenemos que , y como , tenemos que , luego , y , por lo que .

Como los anteriores casos cubren todos los posibles valores de  mayores que , hemos encontrado en todo caso un  tal que  y .

Para los polinomios del tercer tipo, tenemos que si , con  par, entonces  cumple que

.

Entonces, se cumple que .

Como , tenemos que , y como , tenemos que , luego , y , por lo que .

Si , con  impar, entonces

, cumple que

Entonces, se cumple que . Como , tenemos que , y como , tenemos que , si , luego , y , por lo que .

Para el caso , es decir, si , tenemos que, si , entonces el valor anterior:

, cumple que .

Entonces, se cumple que .

Como , tenemos que , y como  se cumple que , por lo que , y entonces , por lo que .

Para los  tales que , se cumple que

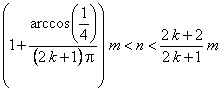 para algún :

Los intervalos 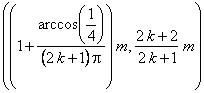 son decrecientes en , y anidados, al ser :

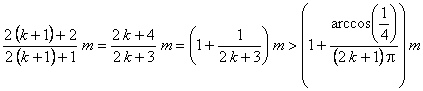Esta desigualdad es equivalente a , es decir

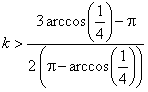, lo que se cumple al ser , y 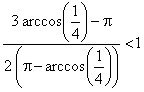 (esta última desigualdad es equivalente a , lo que se cumple al ser ).

Además, el extremo superior del intervalo vale  cuando  vale 1, y los extremos inferiores tienden a 1 cuando  tiende a .

Por tanto, los intervalos 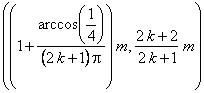 cubren todo el intervalo , y entonces efectivamente para cualquier  tal que , existe algún   de tal forma que .

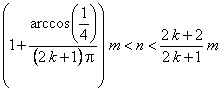Tomando entonces , tenemos que

, y entonces:

.

Esto será mayor que 4 si y sólo si .

Pero como tenemos que 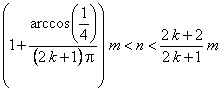, se cumplirá que

, por lo que efectivamente:

. Entonces para los  tales que  también hemos encontrado un  con  y tal que , con lo que hemos terminado.

 

Ejercicio 22.

 

Sea  el anillo de polinomios con coeficientes enteros y sean   polinomios no constantes tales que  divide a  en. Prueba que si  tiene al menos 81 raíces enteras diferentes, entonces el grado de  es mayor que 5.

(2008-Segundo día, Problema 4)

Solución

Sabemos que  con . Así que la ecuación  es cierta para al menos 81 valores de  enteros distintos.

Para esos valores de  tenemos que , así que puesto que esa ecuación se cumple para 81 valores de  enteros distintos, y para cada  de esos solo hay 16 posibilidades, significa que por el 

principio de las casillas, hay al menos 6 valores de  para los cuales  toma el mismo valor, lo que implica que si  no es constante, su grado es mayor que cinco como queríamos probar.