Ejercicio 1.

Encontrar todas las funciones  que sean integrables en cualquier intervalo , que satisfacen la condición para cualquier número real x distinto de 0.

 

 

(7/10/2000-Problema 1)

Solución

 

Si  es integrable en ,  es continua. Como , con  funciones continuas,  es continua en  y si  es continua en un cierto intervalo I,  es diferenciable en dicho intervalo por el Teorema Fundamental del Cálculo Integral, y por tanto  será diferenciable en .

Derivemos entonces a ambos lados de la igualdad:

Por tanto, las funciones que cumplen las condiciones del enunciado son:

 

Ejercicio 2.

Una función derivable  satisface la desigualdad  y al menos para un real  esta desigualdad es estricta, es decir, se cumple que . Demostrar que  no tiene raíces.

(6/10/2001-Problema 2)

Solución

Imaginemos que  sí tiene raíces en los reales. Entonces podemos encontrar un intervalo  de modo que x sea el supremo de las raíces de  en dicho intervalo y además , a no ser que  para todo , caso que no se puede dar porque no se cumpliría . Puesto que  es derivable, también será continua, así que podemos asegurar que existirá un entorno alrededor de x donde la función sea creciente o decreciente (no estrictamente, porque puede tomar valor 0 en más de un punto, pero sí creciente ya que si nunca toma un valor mayor o menor que 0 la desigualdad del enunciado nunca será estricta). Cojamos un punto de ese intervalo, un .

Entonces aplicando el teorema del valor medio de Lagrange, existirá un :

, contradicción, luego  no tiene raíces.

 

Ejercicio 3.

Probar que si  es un polinomio con coeficientes enteros entonces existe un entero  tal que  tiene más de 2003 factores primos distintos.

 

(8/11/2003-Problema 2)

Solución

Vemos un resultado más general: Para todo  existe un entero  tal que  tiene más de  factores distintos. Procedamos por inducción sobre m.

Para m=1 es evidente que existe algún n entero para el cual  tiene al menos un factor primo.

Supongamos que para m=i existe un  tal que  y que  tiene más de i-1 factores primos distintos.

Para m=i+1, bastaría usar que .

Entonces con  queda

 para algún k natural. Y puesto que  son primos relativos, si   tiene i+1 ó más factores primos, luego  tal que  tiene más de m factores primos distintos. Si , es decir, si k=0, tomamos como  el número , ya que . En este caso, el nuevo  sería , y así hasta llegar a un  cuya imagen sea distinta al anterior (existe porque la función es un polinomio no constante). Entonces , y valdría el mismo razonamiento. Otra opción es coger , con  tal que , que también existe.

 

Ejercicio 4.

Sean . Sea  la coordenada x de  y sea  el grado de . Calcular 

(26/11/2005-Problema 1)

Solución

Primero de todo demostremos que  siendo  los términos de la sucesión de Fibonacci (). Esto se puede hacer fácilmente por inducción, ya que para n=1 es cierto, y si suponemos que es cierto para n=i, para n=i+1 se tiene que

Y puesto que  y

, será

.

Por  tanto queda demostrado y como consecuencia  y

 

 

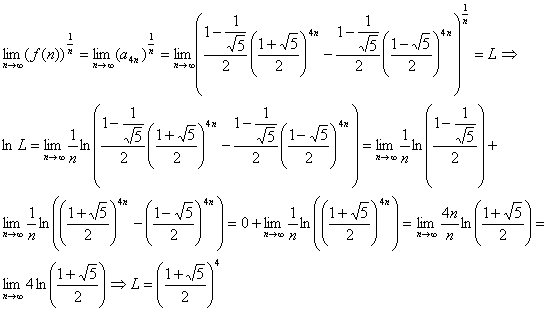
Ejercicio 5.

Considere matrices reales cuadradas  de orden  tales que  y  es simétrica.  Determine si es posible que  sea igual a 

(26/11/2005-Problema 2)

Solución

 

Como el orden de  es impar, entonces  tendrá algún autovalor real, y como , los autovalores de  han de cumplir que , luego entonces  tendrá el autovalor real  . Entonces  tendrá el autovalor , por lo que , y entonces , por lo que  tiene el autovalor 0, y entonces  tiene el autovalor 0. Pero los autovalores de   son de la forma, siendo  autovalor de , luego para un autovalor  de  se cumple que. Pero como ahora demostraremos, la ecuación  no tiene soluciones reales, luego  es complejo puro, contradicción con que  es simétrica y entonces todo los autovalores de  son reales. Por tanto,  no puede tener orden 2005.

Demostremos ahora que la ecuación  no tiene ninguna solución con  real. Esto es evidente ya que

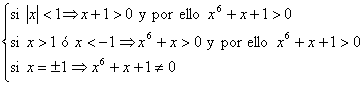
Y por tanto todas las raíces del polinomio son complejas.

 

 

Ejercicio 6.

Considera la sucesión definida de forma recursiva por , y . Calcula  

 

(26/11/2005-Problema 3)

Solución

Expresado en forma matricial, tenemos que 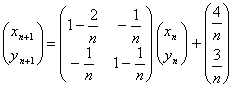. Si llamamos 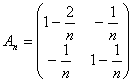, , 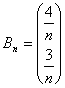la sucesión quedará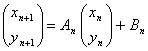 

Iterando la sucesión, tenemos que

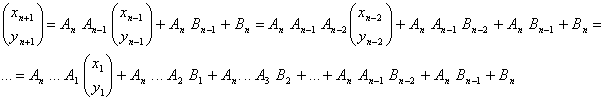
Si llamamos , tenemos entonces que 

Si consideramos ahora la sucesión con la misma ecuación de recurrencia que , pero con , tenemos por lo anterior que esta sucesión se puede expresar en forma explícita como 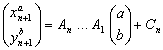. Para hallar , hallamos los autovalores y autovectores de :

: 

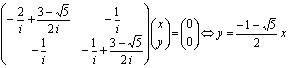
Por tanto, 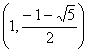 es un autovector de  asociado a 

: 

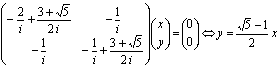
Por tanto, 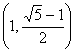 es un autovector de  asociado a 

Entonces, como los autovalores son distintos,  es diagonalizable, siendo

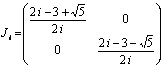, con matriz de paso  (¡no depende de !).

Se cumple entonces que , por lo que

Se cumple que 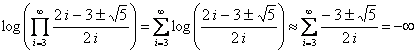 (hemos aplicado la equivalencia  si ), por lo que , y entonces  (O es la matriz nula).

Tenemos entonces que, si existen ,  tales que  tiene límite, se cumplirá que 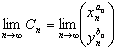, al ser

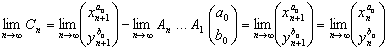
Y en este caso, se cumplirá que 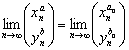 para todo , , ya que

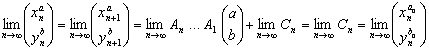
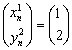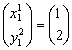Pero nos fijamos en que  para todo : por definición , y si 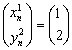, entonces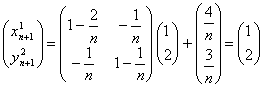 

Por tanto 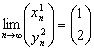, y entonces por lo anterior 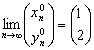. Pero  es la sucesión , por lo que 

 

Ejercicio 7.

Las integrales definidas entre 0 y 1 de los cuadrados de las funciones reales continuas f(x) y g(x) son iguales a 1. Demostrar que existe un número real c tal que

 

.

(17/09/1998-Problema 1)

Solución

Como f y g son continuas,  también es continua. Por tanto  para algún . Además, por la desigualdad de las medias cuadrática y geométrica .

Entonces 

 

Ejercicio 8.

Encontrar el valor de la serie 

 

(02/10/1999-Problema 1)                                                   

Solución

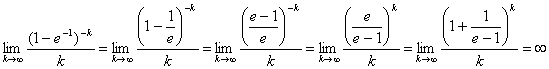 (por ser ).

Por tanto, 

 

Ejercicio 9.

Los vértices de un triángulo ABC pertenecen a la hipérbola . Demostrar que su ortocentro también pertenece a esta hipérbola.

 

(02/10/1999-Problema 2)

Solución

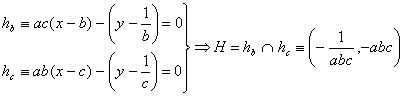Lo haremos por geometría analítica. Sea . El ortocentro  lo podemos calcular como la intersección de las alturas  de ecuaciones: , tras realizar los cálculos pertinentes, y por tanto .

 

Ejercicio 10.

La suma o diferencia (simétrica) de dos conjuntos A y B se define como

 

.

Inicialmente los 1024 subconjuntos de un conjunto de 10 elementos están escritos cíclicamente en una circunferencia. Simultáneamente entre cada dos subconjuntos vecinos se escribe su suma. Después todos los conjuntos anteriores se borran. ¿Qué conjuntos estarán escritos en la circunferencia después de repetir esta operación 2001 veces?

(06/10/2001-Problema 3)

Solución

Denotemos cada subconjunto por un vector  

no pertenece al subconjunto.

Es entonces inmediato que la suma o diferencia simétrica cumple que  se puede calcular simplemente sumando cada componente y expresando el resultado en módulo 2.

Demostremos ahora que en  pasos siendo n el número de elementos del conjunto (en este caso 10), todos los conjuntos escritos en la circunferencia son el conjunto vacío. Esto es equivalente a demostrar que en ese número de pasos, haciendo la operación con la suma habitual de los vectores, todos los vectores que tenemos tienen todas sus componentes con números pares.

Para el caso  se puede comprobar fácilmente que es verdad. Supongamos que es cierto para . Veamos si es cierto también para . Es evidente que para , si en vez de colocar una sola vez los vectores colocamos cada uno dos veces esto sigue siendo cierto, aunque el número de pasos que debemos dar es el doble más 1. Añadámosle a todos los vectores una cifra más, de modo que la mitad sean 0 y la otra mitad sea 1. Entonces, en  pasos las  primeras cifras de los vectores serán nulas (módulo 2). Es inmediato ver que la cifra  también será nula. Basta ver que la última cifra también será nula. Esto es inmediato considerando que es un conjunto de un elemento poniendo en vez de dos veces sus elementos  veces.