Ejercicio 1.
Sean x1 , ... , xn vectores no nulos de un espacio vectorial y 
una transformación lineal que satisface:
(xi) = x1 + x2 + ... + xi , i = 1, .... , n.
Demostrar que los vectores x1 , ... , xn son linealmente independientes.
(10/12/1997-Problema 2)
Solución
Lo demostramos por inducción sobre n = número de vectores:
Si n=1, entonces, como el vector 
es no nulo, es linealmente independiente (l. i.). Lo suponemos cierto para 
vectores que cumplan las condiciones.
Sean n vectores ,..., 
no nulos que cumplen las condiciones, entonces existe una aplicación lineal que cumple que 
,..., 
, por lo que ,..., 
son l. i. (hipótesis de inducción). Por tanto, si ,..., son linealmente dependientes, será el que dependa de los demás, es decir, 
, por lo que, al ser lineal, se cumplirá que
Por otro lado, 
, por lo que igualando tenemos que
.
Entonces tenemos expresado como combinación lineal de ,..., de dos formas distintas, ya que el coeficiente de en la primera forma es 
, y en la segunda es 
, contradicción con que ,..., son l. i. Por tanto, ,..., son l. i.
Ejercicio 2.
Una elipse es reflejada en una recta tangente a ella. La imagen de esta reflexión gira sobre la elipse original (que permanece fija) sin deslizarse. Determinar el lugar geométrico de los focos de la elipse que está rotando.
(10/12/1997- Problema 3)
Solución
Si la elipse inicial la consideramos centrada en el origen y de semiejes 
, 
, entonces su ecuación es 
(si tomamos 
). La elipse que queda al girar la elipse reflejada sobre ésta es simétrica con ésta respecto a su recta tangente, y sus focos serán simétricos a los de esta elipse respecto a la recta tangente. Los focos de esta elipse son 
, 
, y su recta tangente en un punto genérico de ella 
es 
. Para hallar el simétrico respecto a esta recta de un punto cualquiera 
, cogemos la recta perpendicular a esta tangente que pasa por , 
, y hallamos su punto de corte con la tangente:
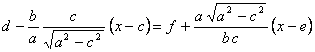, por lo que
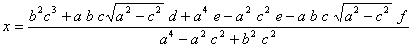
Y sustituyendo en la ecuación de la tangente queda la 
del punto de corte, siendo éste
Entonces el simétrico de respecto la tangente es el simétrico de respecto a este punto de corte 
, que será 
, quedando
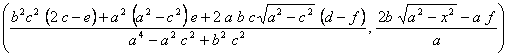
En uno de los focos 
y 
, luego sustituyendo en el punto anterior nos queda que su simétrico será
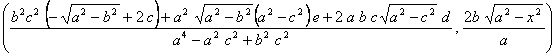, con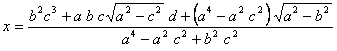 
Como 
es un punto de la elipse, se cumplirá que 
(suponemos 
), luego sustituyéndolo en el punto anterior, nos queda
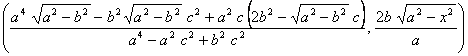, con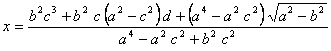 
Ésta es entonces la curva que traza el primer foco, siendo 
el parámetro de la curva (
y 
son fijos, son los semiejes de la elipse inicial). Para los puntos con 
trazará la simétrica a esta curva respecto al eje OX. El otro foco es igual, sólo que 
. Sustituyéndolo en la ecuación del simétrico y haciendo los demás cálculos igual, nos da la curva
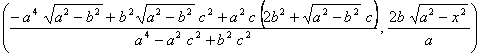
Y como antes su simétrica respecto al eje OX.
Observación: Estas curvas son también elipses. En concreto, si 
, 
quedan las siguientes curvas que describen los focos:
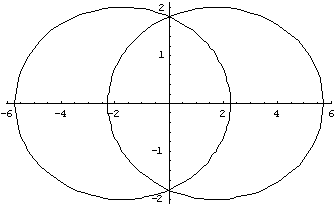
Que son elipses de semiejes 4, 2, el doble que los de la elipse inicial
(Cálculos hechos con ayuda del programa Mathematica).
Ejercicio 3.
Hallar las soluciones de la ecuación: 32x + 3x = 90
(10/05/1999-Problema 1)
Solución
Se cumple que:
(Cogemos sólo la solución positiva porque 
). Entonces 
.
Ejercicio 4.
La víctima de un accidente morirá a menos que reciba en los próximos 10 minutos una transfusión de sangre tipo A-Rh positivo. Se dispone de gran número de donantes de los cuales sólo se sabe que el 40% tienen sangre de ese tipo. Se necesitan dos minutos para determinar el tipo de sangre del posible donante y dos minutos para realizar la transfusión. ¿Cuál es la probabilidad de que se salve si el hospital dispone de un sólo equipo de tipificación de sangre?
(10/05/1999-Problema 2)
Solución
Como tienen 2 minutos para analizar la sangre de cada donante y 2 minutos para hacer la transfusión y en total disponen de 10 minutos, se salvará si el cuarto donante ó alguno de los anteriores tienen sangre A-RH+. Entonces si llamamos 
al suceso “el individuo 
que se analiza tiene sangre A-RH+”, entonces
, siendo 
el suceso “el individuo que se analiza no tiene sangre A-RH+”. Como los sucesos son independientes, ya que la probabilidad de que uno no tenga sangre A-RH+ no se ve afectada por el hecho de que los otros analizados la tengan ó no, la probabilidad de la intersección es el producto de las probabilidades, por lo que:
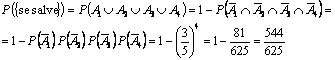
(Ya que el 
tienen sangre A-RH+, por lo que 
).
Ejercicio 5.
Un punto se está moviendo en una recta de tal forma que su velocidad media para cualquier intervalo de tiempo es igual a la media aritmética de las velocidades de los extremos del intervalo. Demostrar que el punto se está moviendo con una aceleración constante.
(10/12/1997-Problema 5)
Solución
La condición es que 
, para todo , con 
. Entonces, variando el punto tenemos que 
para todo 
. Derivando a los 2 lados respecto a 
, tenemos que
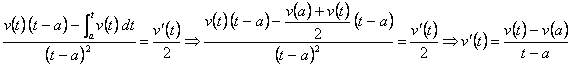Derivando otra vez respecto a , tenemos que
, por lo que 
, y entonces 
es constante.
Ejercicio 6.
Llamaremos número 10-ádico a una sucesión infinita de cifras decimales ...an...a1a0. Los números 10-ádicos se pueden sumar, restar y multiplicar por las mismas reglas que para los números naturales muy grandes. Por ejemplo
...1997 + ...0129 - ...0129 x
...8132 ...8132 ...1997
------- ------- -------
...0129 ...1997 ....903
....61
....1
-------
....613
a) ¿Cuántas soluciones tiene la ecuación x2-x=0 en los números 10-ádicos?
b) Encontrar la suma de todas las soluciones de esta ecuación.
(10/12/1997-Problema 7)
Solución
a) La ecuación 
tiene como soluciones reales 
y 
, que en números 10-ádicos dan 
y 
. Por otro lado, para que el cuadrado de un número
10-ádico 
sea él mismo, se debe cumplir que
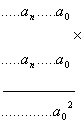sea igual que él mismo, para lo que se debe cumplir que 
(es decir, que 
acabe en la misma cifra que 
). Las únicas cifras que cumplen esto son 
. La única solución que acaba en 0 es la ya hallada : Si existe una solución que acaba en 0 con alguna cifra no nula, sea 
la primera cifra no nula, entonces el número es 
, por lo que
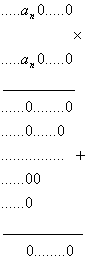
Y entonces 
, contradicción.
La única solución que acaba en 1 es la ya hallada : Si existe una solución que acaba en 1 con alguna cifra no nula aparte del 1, sea la primera cifra no nula aparte del 1, entonces el número es 
, por lo que
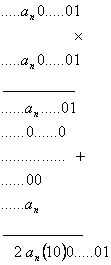
Entonces, para que el cuadrado del número sea él mismo, se debe cumplir que
, es decir, que 
, por lo que , contradicción. Vemos que sólo hay una solución que acabe en 5: La cifra n-ésima del cuadrado del número 
es
(Donde en cada término está incluido lo que te llevabas de la operación anterior, por ejemplo, en 
está incluido lo que te llevabas de 
)
Como 
, se cumple que
.
Entonces, para que la cifra n-ésima sea igual en los 2 números, se ha de cumplir que 
, lo que da una única solución .
Vemos que también hay una única solución que acaba en 6: La cifra n-ésima del cuadrado del número 
es
(Donde en cada término está incluido lo que te llevabas de la operación anterior, por ejemplo, en 
está incluido lo que te llevabas de 
)
Como 
, se cumple que
.
Entonces, para que la cifra n-ésima sea igual en los 2 números, se ha de cumplir que
Lo que da una única cifra solución 
. Por tanto hay 4 soluciones a la ecuación.
b) Para hallar su suma vemos que el número que acaba en 5 y el que acaba en 6 suman 
. Para ello, si llamamos 
al número que acababa en 5, vemos que 
acaba en 6: 
y además cumple que
(La penúltima igualdad es porque ). Entonces el cuadrado de es él mismo, luego es la solución que acaba en 6, y entonces 
. Como 
, la suma de las 4 soluciones es 
. (En los números 10-ádicos, como en los números normales, todo número tiene su opuesto 
que sumado a él da 
: no hay más que aumentar las cifras de lo justo para que den 0, y se cumple también la propiedad distributiva, luego se puede desarrollar 
).
Ejercicio 7.
Sea a1, a2, a3, a4, a5, a6 una progresión geométrica de razón r. Si a1 + a2 + a3 + a4 + a5 = 3124, y a2 + a3 + a4 + a5 + a6 = 2343, hallar r y a3.
(10/05/1999-Problema 3)
Solución
Si a la razón de la progresión geométrica la llamamos 
, se cumple que 
.
Entonces 
.
Por otro lado, como 
,
. Igualando las 2 ecuaciones, tenemos que
.
Sustituyéndolo en la primera ecuación, tenemos que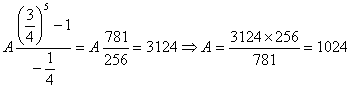 
. Entonces 
.
Ejercicio 8.
Para la construcción de una pista circular de patinaje sobre hielo, se tienen las propuestas de dos empresas. La empresa A cobra $40 por m2 de pista, $30 el metro de cerco y un adicional fijo de $400 para gastos generales. La empresa B cobra $36 por m2 de pista, $40 el metro de cerco y un adicional fijo de $1200. ¿Para qué valores del diámetro de la pista es más ventajoso contratar a la empresa A?
(10/05/1999-Problema 4)
Solución
Lo que cobra la primera empresa es 
, y lo que cobra la segunda 
. Para que sea más ventajoso contratar a la primera empresa, ha de ser
La ecuación 
tiene como soluciones
, luego la inecuación tiene como solución 
.
Como 
, lo de la izquierda de es negativo, por lo que al ser un radio, y por tanto positivo, siempre se cumplirá que 
. Entonces será más ventajoso contratar a la primera empresa cuando 
, es decir, cuando el diámetro sea menor que 
.
Ejercicio 9.
¿Cuál es la probabilidad de que las fechas de nacimiento de 4 personas tomadas al azar correspondan todas a dos meses cualesquiera del año quedando exactamente 10 meses libres? (Suponer que todos los meses tienen la misma probabilidad.)
(10/05/1999-Problema 5)
Solución
La probabilidad de que hayan nacido las 4 personas en, por ejemplo, Enero y Febrero es
(ya que son sucesos disjuntos, luego la probabilidad de la unión es la suma de las probabilidades).
Se cumple que:
(Ya que son sucesos independientes, luego la probabilidad de la intersección es el producto de las probabilidades. La probabilidad de nacer en cualquier mes es 
, ya que los 12 meses tienen la misma probabilidad). Se puede ver de forma análoga que la probabilidad de cada uno de los otros 2 sucesos también es 
, luego
Habrá la misma probabilidad de que los 4 hayan nacido en otros 2 meses del año. Como el número de formas de tomar 2 meses de los 12 del año es
,
se cumple que 
.
Ejercicio 10.
Sean x y d números naturales tales que el resto de dividir x por d es igual a 4 y el resto de dividir 14x por d es 17. Hallar el resto de dividir 210x por d.
(10/05/1999-Problema 7)
Solución
Como el resto de dividir entre 
es 4, se cumple que 
. Como el resto de dividir 
entre es 17, se cumple que 
. Sustituyendo el de la primera congruencia en la segunda, queda que 
. Como el divisor es siempre mayor que el resto y el resto de dividir entre es 17, se cumple que 
y 
. Entonces para hallar el resto de dividir 
entre 39, hacemos la congruencia de módulo 39: 
(ya que al dividir 840 entre 39 da de resto 21). Por tanto, el resto de dividir entre 39 es 21.
Ejercicio 11.
Encontrar el máximo valor que puede tomar el siguiente determinante, si se sabe que cada una de sus componentes es alguno de los números reales 0 ó 1:
(30/08/2001-Problema 1)
Solución
Es fácil ver que podemos conseguir que el determinante dé 2, bastaría elegir la matriz:
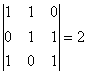. Veamos que es imposible que el determinante sea mayor que 2. Es obvio que el valor absoluto del determinante sólo puede valer 0, 1, 2 ó 3. Tenemos que demostrar entonces que es imposible que tome el valor 3. Supongamos que lo tomara. Entonces:
,
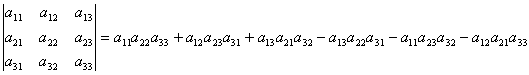y necesariamente 
y para ello todos los 
, así que el determinante daría 0 en contra de lo supuesto. Por tanto el valor máximo es 2.
