Ejercicio 1.

Sea  un número natural. Probar que: .

Propuesto por José Luís Díaz Barrero

Solución

La primera desigualdad es equivalente a . Si dividimos entre  en el numerador y denominador de lo de dentro de , nos queda:

.

Si consideramos la partición  del intervalo , lo que tenemos es la suma inferior de la función  en ese intervalo, ya que esa función es decreciente en  (, ya que  está entre 0 y  cuando  está entre 0 y 1, por lo que la  es positiva), y la estamos evaluando en los extremos superiores de los subintervalos, por lo que

.

La segunda desigualdad es equivalente a . Si dividimos entre  en el numerador y denominador de lo de dentro de , nos queda:

.

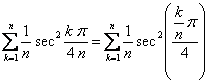Si consideramos la partición del intervalo : , lo que tenemos es la suma superior de la función  en ese intervalo, ya que esa función es creciente en

(, ya que  está entre 0 y  cuando  está entre 0 y 1, por lo que la  es positiva), y la estamos evaluando en los extremos superiores de los subintervalos, por lo que

.

 

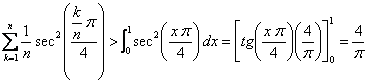Ejercicio 2.

Sea  un polígono regular inscrito en una circunferencia centrada en el origen y de radio . Si  es un punto cualquiera cuya distancia al origen es menor o igual que , probar que:

 

(Propuesto en  La Gaceta de la R.S.M.E. Problema 40)

Solución

Coloquemos los ejes de coordenadas  de modo que  sea el punto .

Entonces, si P dista  del origen (con ) tenemos que:

Y por tanto se obtiene fácilmente que:

Para demostrar la otra parte de la desigualdad probaremos primero que si tenemos un triángulo ABC con la base BC fijada y con AB+AC=cte, entonces, el triángulo tendrá área máxima si es isósceles, o dicho de otro modo, si tiene base BC fijada y un área dada, su perímetro será mínimo si es isósceles.

En este caso, como la única forma de que todos los triángulos sean isósceles es que P sea el centro del polígono (para el cual la suma de AB+AC=2R para cada uno de los triángulos ), si P es distinto del centro como el área de los triángulos es mayor o igual que el área del polígono y el lado  también, tenemos que .

La demostración de que si un triángulo tiene un lado  fijado y la suma de los dos opuestos  también fijada, entonces el área es máxima si  se puede hacer fácilmente usando la fórmula de Heron:

 y el punto es un máximo, lo cual se puede ver fácilmente volviendo a derivar la expresión y teniendo en cuenta que .

 

Ejercicio 3.

Sean  para , con  y . Probar que

 

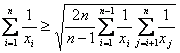
(Propuesto en La Gaceta de la R.S.M.E.- Problema 36)

Solución

Si elevamos al cuadrado en la desigualdad que queremos demostrar y reagrupamos los términos conseguimos:

 

 

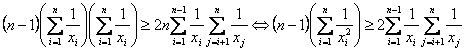
Demostremos que la última desigualdad es cierta. Si consideramos las sucesiones , la desigualdad anterior quedaría escrita como:

 

, donde en el primer lado tenemos  términos y en el segundo , es decir, tenemos  sucesiones  en cada término, siendo   y como en el primer término  y en el segundo , por la desigualdad de reagrupamiento la desigualdad es cierta, alcanzándose la igualdad si y sólo si  , esto es si , es decir si  es constante.

 

Ejercicio 4.

Sean a, b, c los lados de un triángulo. Probar que

 

Solución

Puesto que a, b, c son los lados de un triángulo, entonces se cumple que .

Como la desigualdad es simétrica, podemos suponer sin pérdida de la generalidad que . Entonces, se tiene que

Observación

Es conocida la siguiente cota inferior para la expresión de la izquierda:  (desigualdad de Nesbitt)

 

Ejercicio 5.

Sea  entero,  y . Prueba que

,  y

Solución

Las desigualdades son homogéneas, esto es, si tenemos ciertos números  que cumplen la desigualdad, entonces  también la cumplen. Así que podemos suponer por ejemplo que  sin pérdida de la generalidad.

Entonces la primera desigualdad queda:

.

Como  son todos mayores que cero porque  son menores que 1, la desigualdad es equivalente a:

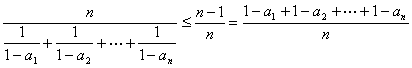, y por tanto es una aplicación directa de las desigualdades de las medias.

Con la segunda actuaremos de la misma forma:

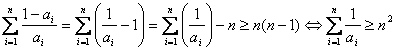
que se obtiene directamente de aplicar la desigualdad entre las medias aritméticas y armónica.

Probemos ahora la tercera desigualdad:

. Lo haremos por la desigualdad de reagrupamiento. Tenemos dos series multiplicadas:  y como la desigualdad es simétrica podemos suponer sin pérdida de la generalidad que . Como las dos series están ordenadas de la misma forma, el producto que tenemos es mayor que si lo reagrupamos de cualquier otra forma:

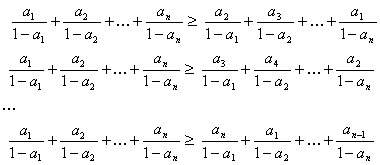
Y si las sumamos todas queda que

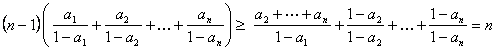, y queda probado.

 

Ejercicio 6.

Sean  números reales positivos y sea  una función continua. Prueba que existe un  tal que .

 

(Propuesto por José Luís Díaz Barrero)

Solución

Hay que ver que existe un  tal que

.

Si tomamos , con , hay que ver que existe un  tal que . Se cumple que  es continua en , ya que lo es  y no se anulan los denominadores. Vemos cuál sería el límite de  en :

.

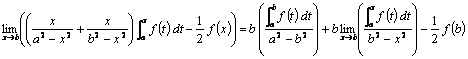Este límite será  si ,  si .

Además, se cumplirá que la función  es mayor que 0 si  y menor que 0 si  , ya que es estrictamente creciente:

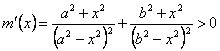, y se anula en :

.

Si existen al menos 2 valores  tales que , , entonces existen 2 casos: si para todos  tales que ,  existe un  tal que , entonces los ceros de la función   son densos en  (esto es porque, si existe un intervalo  en el que no hay ceros de , entonces si consideramos el mínimo cero de  en   que sea mayor ó igual que , que existirá por continuidad de la función  y porque al menos hay un cero de  en   que sea mayor ó igual que : , y el máximo cero de   en   que sea menor ó igual que , que existirá por continuidad de la función  y porque al menos hay un cero de  en   que sea menor ó igual que : , entonces entre ellos tendrá que haber un cero de , que por tanto será mayor que  y menor que , luego estará en , contradicción) por lo que, al ser  continua, se cumplirá que  para todo , por lo que, al ser  continua,  para todo , y entonces   para todo .

Si existen  tales que ,  y no existe un  tal que , entonces tenemos otros 3 casos: Si existe una sucesión  con , siendo , y , entonces  por continuidad de , luego

, con .

Si existe una sucesión  con , siendo , y , entonces  por continuidad de , luego , con .

Si no se dan los dos casos anteriores, existirá un entorno cercano a , llamémosle , en el que , ó bien , por continuidad de . Por lo mismo, existirá un entorno cercano a , llamémosle , en el que , ó bien . Si, por ejemplo,  y , entonces  es estrictamente creciente en  (ya que, al ser  continua,  ),  es estrictamente creciente en . Pero entonces,  para todo ,  para todo , luego por el teorema de Bolzano habrá un  entre medias de los dos , y por tanto entre , , en el que , contradicción, por lo que  cambia de signo en los 2 entornos, y entonces por continuidad de , si , se cumplirá que

, por lo que

Y entonces por Bolzano existe  tal que  (los casos  ó  ya fueron estudiados antes).

Si  tiene como mucho una raíz en , entonces por continuidad de la función integral existirá un entorno  en el que  para todo , ó bien  para todo . Si  para todo  entonces se cumplirá que existirá un  tal que , si : Si  para todo , entonces , contradicción. Se cumplirá además que  si tomamos  suficientemente cercano a , por lo que

. Entonces si , se cumple que

,  es continua en , por lo que por Bolzano existe un  tal que . Si , entonces, como , por continuidad de la función integral existirá algún  tal que  (Bolzano), que podrá ser  ó el  único posible  que estamos suponiendo tal que . Supongamos que  es el menor de los dos posibles.

Entonces : Si , entonces por continuidad de  existe un  tal que  para todo , por lo que , y entonces

, por lo que por el razonamiento anterior existe un  tal que , con , contradicción con que  era el mínimo.

Entonces, tenemos que , por lo que por Bolzano existe un  (si ) tal que . Si  pero , entonces , por lo que podemos también aplicar Bolzano para encontrar un  tal que .

Si  y , es decir, si  es el único valor para el que , y además , entonces en principio no podemos aplicar Bolzano en . Pero entonces se cumplirá que  para todo , ya que si existe un  tal que , entonces por Bolzano existirá un  tal que , contradicción con que  era el único.

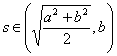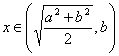Además debe existir un  tal que , ya que si  para todo , entonces , por lo que

, contradicción con lo anterior.

Pero entonces , por lo que existe un  tal que  (Bolzano).

El caso  es igual que el caso , invirtiendo todas las desigualdades (salvo las de la función ), teniendo en cuenta que, si , entonces .

Ejercicio 7.

Hallar todas las tales que  

 

Solución

Sustituyamos algunos valores:

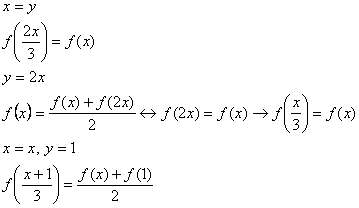
Vamos a utilizar las igualdades anteriores para ver que  para todo : Para  es obvio, y si , entonces

Para los números negativos:

(Sabemos que porque  al ser )

 

Ejercicio 8.

Encuentra todos los polinomios  tales que

Solución

(Al ser  un polinomio, se cumple que si  para todo , entonces  para todo )

 

Ejercicio 9.

Encontrar todas las funciones  estrictamente crecientes tales que

 

(Ecuación Funcional de Cauchy)

Solución

 

 sección 2.3

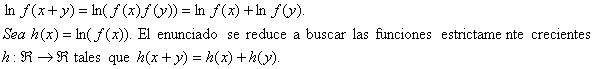
Por tanto,

Observaciones

1) Podemos tomar logaritmos porque  para todo : si   para todo , no se podría cumplir la ecuación . Si existen ,  tales que  y , sea  tal que  y  (existe tal  porque  es estrictamente creciente), entonces , contradicción

( es positivo ya que, al ser  estrictamente creciente, tenemos que ; se cumple que , al ser  para todo , y no ser  constantemente 0)

2) En la sección 2. 3 resolvimos la ecuación  para  Hay que resolverla en este problema para ,  estrictamente creciente. Una forma de hacerlo es:

Podemos poner  como , donde  también cumple que , por lo que también será  para todo . Entonces, al ser  estrictamente creciente y ,  enteros, se cumple que

, por lo que

, siendo  la parte fraccionaria. Como ésta está entre 0 y 1, tenemos que  para todo . Entonces, para todo  se cumple que , por lo que necesariamente , y entonces  para todo .

Si , con  y , tenemos que , por lo que , y entonces  para todo

Tenemos entonces que, si , existe una sucesión  tal que  y  para todo , con , por lo que

. Por otro lado, existe una sucesión  tal que  y  para todo , con , por lo que

. Tenemos entonces que , por lo que, tomando límites, tenemos que

, y entonces  para todo

 

Ejercicio 10.

Sean a, b, c tres enteros distintos, y sea P un polinomio con coeficientes enteros. Prueba que las condiciones ,  y  no pueden cumplirse simultáneamente.

 

Solución

Sabiendo que  divide a  y  divide a  y  divide a  (en un polinomio con coeficientes enteros se tiene que ) se llega a que  lo cual implica que  todos los términos tienen que ser iguales y por tanto , en contra de lo supuesto.