La desigualdad más básica que se puede usar en un problema es 
ó también 
. Sin embargo, convertir una desigualdad dada en una suma de números cuadrados puede ser una tarea muy complicada. Por eso algunas estrategias pueden ser bastante útiles.
Por ejemplo, con 
sabemos que
, que es una desigualdad muy interesante, que por ejemplo en el caso particular en que 
lleva a 
.
En muchos problemas, conocer alguna de estas desigualdades nos puede ahorrar mucho trabajo para llegar a la solución.
Otras desigualdades sencillas que podemos obtener siguiendo un procedimiento similar son:
, y la última desigualdad se conoce como la desigualdad entre las medias aritmética y geométrica.
Claramente la igualdad se alcanza en las desigualdades anteriores sólo cuando 
.
Esta desigualdad se puede generalizar a más números y a otros tipos distintos de medias:
2. 2. 1. Desigualdad de las Medias:
Sean n números 
. Entonces se tiene que:
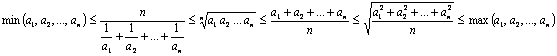
Esta desigualdad se llama también la desigualdad Mh, Mg, Ma, Mc ya que relaciona las medias armónica, geométrica, aritmética y cuadrática respectivamente.
En general se cumple la desigualdad 
siendo
.
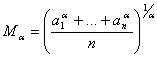La desigualdad anterior es un caso particular entonces para 
.
La igualdad entre todas las medias se alcanza solamente cuando todos los números son iguales.
Ejemplo:
Sean 
n números reales positivos.
Demuestra que si 
entonces 
Usaremos la desigualdad de las medias. Sabemos que:
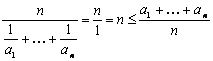, y esto es equivalente a 
2. 2. 2. Desigualdad de Reagrupamiento (Rearrangement principle)
Otra desigualdad muy interesante y bastante sencilla es la siguiente: Imaginemos que tenemos tres sacos con billetes, uno de 500 euros, otro de 200 euros y otro de 100 euros y nos dejan coger de un saco cinco billetes, de otro tres y de otro uno. Evidentemente, para sacar el máximo dinero posible, cogeremos 5 billetes de 500 euros, 3 billetes de 200 euros y 1 billete de 100 euros.
Este ejemplo se puede generalizar. En general si tenemos dos sucesiones ordenadas en el mismo orden (las dos crecientes o las dos decrecientes) la suma del producto de los términos es máxima si tomamos el mayor por el mayor, el siguiente mayor por el siguiente mayor y así hasta el menor por el menor, y la suma de los productos será mínima si multiplicamos el mayor por el menor, el siguiente mayor por el siguiente menor y así hasta el menor de la primera sucesión por el mayor de la última. Esto se puede formalizar como:
Si las secuencias A y B están ordenadas en el mismo orden:
, entonces 
Donde 
es una cierta permutación, esto es 
, siendo
una función biyectiva.
La igualdad se alcanza cuando todos los términos de cada sucesión son iguales.
Por ejemplo:
Si tenemos la secuencia a, b, c y la secuencia a, b, c de nuevo,
Ya que en el primer caso hemos ordenado las dos secuencias en el mismo orden.
Esto se puede escribir de forma compacta como: (ver [1])
También es fácil ver que
, ó, expresado con matrices:
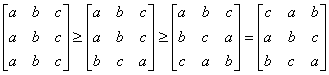
2. 2. 3. Desigualdad de Jensen:
Esta desigualdad nos da una relación entre la media de las imágenes de una función y la función de la media.
, si la función 
es convexa, esto es, si la segunda derivada de es negativa. Esto se puede observar muy bien en un gráfico:
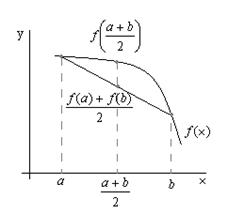
La desigualdad en general se cumple si tenemos una combinación lineal de 
, …, 
con suma de coeficientes 1. Si la función es cóncava, la desigualdad cambia de sentido.
Ejemplo:
Sean a, b, c números reales positivos que satisfacen la relación 
.
Probar la desigualdad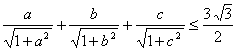 
Haciendo el cambio de variable 
con A+B+C=180º (esta última igualdad implica que ), la parte izquierda de la desigualdad queda:
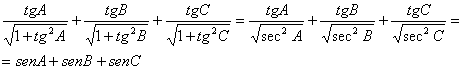
Y utilizando la desigualdad de Jensen, como el seno es una función convexa en 
,
.
Nota:
Es muy común usar cambios de variable como hemos hecho en este problema.
Tenemos una condición, con la que es difícil de trabajar.
Si multiplicamos a los dos lados por 
la condición queda como: 
, y sabemos que 
, por tanto, el cambio de variable 
, nos facilita el problema porque la condición deja de ser 
para ser 
, con la que es mucho más fácil trabajar.
