Muchos problemas propuestos en olimpiadas matemáticas se pueden resolver contando las formas posibles de realizar una determinada acción, o, utilizando el camino inverso, interpretar una fórmula que nos dé el enunciado como el cardinal de un conjunto. Por ejemplo, si los dos miembros de una identidad que nos piden verificar son distintas formas de contar una misma cosa, es evidente que la identidad se cumple.
Hay muchas herramientas para contar. La combinatoria nos ofrece numerosas fórmulas para contar las distintas posibilidades para ordenar objetos, y la mayoría están recogidas en casi todos los libros de cálculo ó de matemática discreta ([4], [5]).
También es útil conocer los números combinatorios, y algunas de las relaciones que satisfacen. Enumeraremos algunas de ellas, por ejemplo:
Que se pueden probar fácilmente por inducción. Demostraremos la última fórmula ya que se puede dar una prueba bastante curiosa:
Sabemos que por el binomio de Newton: 
. Sustituyendo ahora por 
obtenemos precisamente 
.
Otra herramienta muy conocida para contar es el Principio de las Casillas o Principio de Dirichlet, también conocido como el Principio del Palomar y The Box Principle. El enunciado de este principio es muy sencillo, una primera versión podría ser: “Tenemos cinco flores y cuatro jarrones. Si colocamos las flores en cuatro jarrones, entonces en al menos un jarrón habrá al menos dos flores”. Como se puede ver por el enunciado, es un principio bastante intuitivo.
Una versión más general sería: “Si tenemos 
objetos, y 
cajas en las que distribuirlos, al menos en una de ellas habrá 
objetos”, donde 
denota el menor número entero 
.
Un ejemplo de utilización de este principio en un problema nada trivial sería:
Se consideran cuatro números reales y distintos del intervalo (0,1).
Demostrar que siempre se pueden elegir dos de ellos, a y b, tales que:
Todos los números del intervalo (0,1) son de la forma 
, con 
.
Dividiendo en tres partes dicho intervalo: 
, 
, 
, por el principio del palomar tenemos que al menos dos de los cuatro números considerados, 
y 
verifican: 
.
Entonces, como la función coseno es decreciente en 
, suponiendo sin pérdida de generalidad que 
, tenemos que 
, por lo que
, desigualdad que con 
y 
queda:
, que es a su vez equivalente a
Finalmente, para obtener la desigualdad del enunciado, dividimos por 
esta última expresión.
Como ejemplo puede servir el siguiente problema:
Considera los conjuntos:
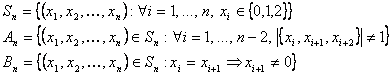
Prueba que 
(IMC 2005-Problema 2, primer día)
Para n=2 es cierto, ya que
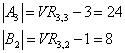
También se cumple para n=3.
Supongamos que es cierto para todo 
, 
. Entonces, demostremos que también es cierto para 
. Contemos los elementos que hay en cada conjunto por medio de relaciones de recurrencia de segundo orden:
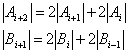
Comprobamos que se cumplen estas dos igualdades:
= nº de vectores de 
con las dos últimas cifras distintas y que por tanto les puedo añadir como última cifra la última que tengan.
= nº de vectores de a los que le añado de última cifra una de las dos cifras en las que no acaban
(Otra forma de verlo sería que por cada vector en 
puedo conseguir 2 vectores en 
metiendo 2 veces una cifra distinta a la última del vector en , y por cada vector en 
puedo conseguir 2 vectores en metiendo al final una cifra distinta a la última del vector en . Son distintos a los vectores en conseguidos antes, porque estos tienen las 2 últimas cifras distintas, y los anteriores tenían las 2 últimas cifras iguales, y todo vector de se puede conseguir así, luego 
).
= nº de vectores de 
con la última cifra distinta de 0 y que por tanto les puedo añadir un 0.
= nº de vectores de a los que le añade un 1 o un 2.
Por lo que se cumple también la segunda igualdad
Y por tanto se cumple la igualdad del enunciado (inducción).
