2.3. Ecuaciones Funcionales.
Las ecuaciones funcionales son ecuaciones en las que tenemos una relación entre una función en un punto ó en varios, y sus derivadas ó sucesivas evaluaciones.
Pondremos varios ejemplos para que se puedan ver distintas formas de abordar un problema de este tipo:
Encontrar todas las funciones 
tales que 
Para empezar, como tenemos x e y podemos probar a hacer algunas sustituciones con números.
Lo primero de todo, llamemos 
. Entonces es fácil ver que con 
, obtenemos:
Ahora que sabemos los valores de 
, podemos probar con 
:
Parece evidente que si 
, se cumplirá que 
para todo 
, así que intentemos probarlo por inducción.
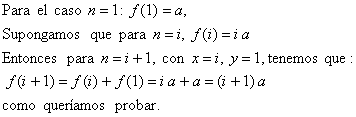
Así que todas las funciones posibles son 
Observación
Las funciones 
que cumplen que son también 
, ya que, sea 
con 
, se cumple que
, por lo que 
(tenemos que 
, porque 
. Se cumple que 
)
Hallar todas las funciones 
tales que
.
Sustituyendo x por y obtenemos que:
Encontrar todas las funciones 
tales que 
(OME-fase nacional 2001)
Supongamos que existe una función tal que .
Entonces, si
, se cumple que
Por lo que tenemos que 
, y además 
Pero entonces, haciendo 
en la primera igualdad y 
en la segunda, tenemos que 
, por lo que 
, contradicción con que 
.
Por tanto, no existe ninguna función que cumpla las condiciones del enunciado.
