Ejercicio 1
Sea ![]() y supongamos que existe un
y supongamos que existe un ![]() ,tal que
,tal que
![]()
para todo ![]() . ¿Es cierto entonces que
. ¿Es cierto entonces que ![]() para todo
para todo ![]() ?
?
(Definición de ![]() ; Una función pertenece a
; Una función pertenece a ![]() si su derivada es continua en
si su derivada es continua en ![]() )
)
(30/7/1994-Problema 1)
Solución
Supongamos que no fuera cierto, esto es, que existiera un cierto ![]() para el cual
para el cual ![]() .
.
Subdividimos el intervalo![]() en intervalos de la forma
en intervalos de la forma![]() , con
, con ![]() , siendo
, siendo ![]() la parte entera. Entonces habrá un mínimo
la parte entera. Entonces habrá un mínimo ![]() con
con ![]() tal que
tal que ![]() y en el intervalo
y en el intervalo ![]() existe un
existe un ![]() tal que
tal que![]() . Por simetría en el razonamiento supongamos que
. Por simetría en el razonamiento supongamos que ![]() . Puesto que estamos trabajando con una función continua en un intervalo cerrado y acotado,
. Puesto que estamos trabajando con una función continua en un intervalo cerrado y acotado, ![]() , ó
, ó ![]() si el mínimo
si el mínimo ![]() es
es ![]() , alcanzará el máximo absoluto, y además, sabemos que este máximo es estrictamente mayor que 0. Sea
, alcanzará el máximo absoluto, y además, sabemos que este máximo es estrictamente mayor que 0. Sea ![]() y
y ![]() el mínimo punto del intervalo
el mínimo punto del intervalo ![]() en el que
en el que ![]() alcanza su máximo, que existirá porque
alcanza su máximo, que existirá porque ![]() es continua.
es continua.
Entonces por el teorema de Lagrange tendremos que existe un ![]() tal que
tal que 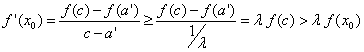 , contradicción, por lo que
, contradicción, por lo que ![]() para todo
para todo ![]() .
.
![]() una función dada por
una función dada por ![]()
a) Prueba que ![]() alcanza su mínimo y su máximo absoluto.
alcanza su mínimo y su máximo absoluto.
b) Determina todos los puntos ![]() tales que
tales que ![]() y determina para cuáles de ellos
y determina para cuáles de ellos ![]() alcanza un extremo relativo o absoluto.
alcanza un extremo relativo o absoluto.
(30/7/1994-Problema 2)
Solución
a) La función ![]() es una función diferenciable, y por tanto continua, en el plano.
es una función diferenciable, y por tanto continua, en el plano.
Puesto que f es una función continua, en un círculo centrado en el origen y de radio 1 alcanzará su máximo y su mínimo absoluto. Demostremos que en el complementario del círculo la función está acotada entre [-1/e, 1/e]:
Es evidente, ya que 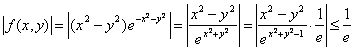 , al ser
, al ser 
![]() . Por tanto, como en el círculo de radio 1 se alcanzan los valores f(1,0)=1/e, f(0,-1)=-1/e, la función alcanza su máximo y mínimo absoluto.
. Por tanto, como en el círculo de radio 1 se alcanzan los valores f(1,0)=1/e, f(0,-1)=-1/e, la función alcanza su máximo y mínimo absoluto.
b) Calculemos ahora sus derivadas parciales:
![]() .
.
Es fácil ver que éstas son iguales a 0 si y sólo si:
![]() .
.
Basta con sustituir y encontrar el valor de f en cada punto para ver que:
f(1,0)=f(-1,0)=1/e son máximos absolutos y que f(0,1)=f(0,-1)=-1/e son mínimos absolutos, ya que f(0,0)=0. El punto (0,0) se comprueba con la matriz Hessiana que es un punto de silla, esto es no es máximo ni mínimo local ni absoluto.
Otra forma de hacerlo:
Vimos en la primera solución que (1,0), (-1,0), (0,1), (0,-1) y (0,0) son los puntos críticos de f. Con la matriz Hessiana se puede ver que en (1,0), (-1,0) se alcanzan máximos relativos, en (0,1), (0,-1) se alcanzan mínimos relativos y (0,0) es un punto de silla. Vamos a ver que en (1,0), (-1,0) f. alcanza su máximo absoluto, y que en (0,1), (0,-1) f alcanza su mínimo absoluto, por lo que la función alcanza su máximo y mínimo absoluto:
Para ello, hay que ver que ![]()
![]() , y que
, y que ![]()
![]() .
.
La primera desigualdad es equivalente a ![]() . Entonces, como
. Entonces, como ![]() , basta con ver que
, basta con ver que ![]() . Si hacemos el cambio de variable
. Si hacemos el cambio de variable ![]() , esta última desigualdad queda
, esta última desigualdad queda ![]() , luego basta con ver que
, luego basta con ver que ![]() para todo
para todo ![]() . Pero
. Pero ![]() si
si ![]() ,
, ![]() si
si ![]() , por lo que
, por lo que ![]() tiene el mínimo global en el 1, y entonces
tiene el mínimo global en el 1, y entonces ![]() , como queríamos.
, como queríamos.
La segunda desigualdad es equivalente a ![]() . Entonces, como
. Entonces, como ![]() , basta con ver que
, basta con ver que ![]() , es decir, que
, es decir, que ![]() , lo que ya hemos visto para demostrar la primera desigualdad.
, lo que ya hemos visto para demostrar la primera desigualdad.
![]() una secuencia de números reales positivos tales que
una secuencia de números reales positivos tales que ![]() . Halla
. Halla ![]() donde ln denota el logaritmo neperiano.
donde ln denota el logaritmo neperiano.
(1997-Primer día, Problema 1)
Solución
![]() es una suma de Riemann de
es una suma de Riemann de ![]() en
en ![]() , por lo que:
, por lo que:
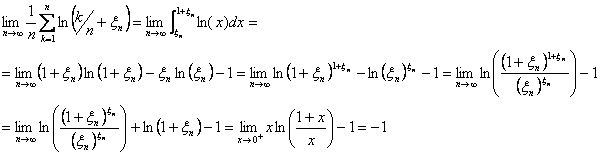
(En la última igualdad hemos aplicado la regla de L’Hopital a la función 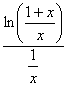 )
)
Supongamos que ![]() es convergente. ¿Son las siguientes sumas también convergentes?
es convergente. ¿Son las siguientes sumas también convergentes?
a) ![]()
b) ![]()
(1997-Primer día, Problema 2)
Solución
a) Sea ![]() y
y ![]() , donde
, donde ![]() es la sucesión que debemos sumar.
es la sucesión que debemos sumar.
Entonces ![]() para
para ![]() . (Ya que entre los términos
. (Ya que entre los términos ![]() y
y ![]() , se suman todos los términos entre
, se suman todos los términos entre ![]() y
y ![]() )
)
Como ![]() converge
converge![]() , donde
, donde ![]() , y como
, y como ![]() , con
, con
![]() , al ser
, al ser ![]() convergente, podemos ver que
convergente, podemos ver que
![]() , ya que
, ya que ![]()
Entonces la suma del apartado a) es convergente.
Otra forma de verlo es: Como ![]() y
y ![]() converge, por lo que
converge, por lo que ![]() , y como
, y como ![]() ,
, ![]() cuando
cuando ![]() , se cumple que:
, se cumple que:
![]() , por lo que
, por lo que
![]()
b) No se cumple necesariamente: la suma ![]() con
con 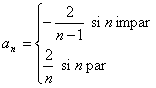
converge por el criterio de Leibniz y la serie del apartado b) no converge.
Otra forma de verlo: Si agrupamos los términos con – y los que tienen +, la serie del apartado b) se puede poner como ![]() . Operando ahora impares con pares, queda que esto último es igual a:
. Operando ahora impares con pares, queda que esto último es igual a:
![]() . Esto es una serie de términos negativos, pero si consideramos la serie correspondiente de términos positivos, queda que
. Esto es una serie de términos negativos, pero si consideramos la serie correspondiente de términos positivos, queda que ![]() si
si ![]() , por lo que:
, por lo que:
![]() , serie divergente, por lo que por el criterio de comparación
, serie divergente, por lo que por el criterio de comparación ![]() es divergente, y entonces la serie que nos dan es divergente.
es divergente, y entonces la serie que nos dan es divergente.
Sea M una matriz invertible de dimensión ![]() , representada, en bloques de la siguiente forma:
, representada, en bloques de la siguiente forma: ![]() , y
, y ![]()
Demuestra que ![]() .
.
(1997-Segundo día, Problema 2)
Solución
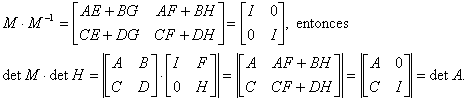
a) Sea la aplicación lineal ![]() del espacio
del espacio ![]() de matrices
de matrices ![]() con entradas reales, esto es:
con entradas reales, esto es:
(1) ![]() para todo
para todo ![]() . Prueba que existe una única matriz
. Prueba que existe una única matriz ![]() tal que
tal que ![]() para toda
para toda ![]()
b) Supongamos además de (1) que
(2) ![]() para todas
para todas ![]() . Prueba que existe
. Prueba que existe ![]() tal que
tal que ![]() para toda
para toda ![]()
(1997-Segundo día, Problema 4)
Solución
a) Primero probaremos que si C existe, entonces C es única. Después probaremos que la matriz ![]() existe.
existe.
i) C es única:
Sea ![]() una matriz cuyo elemento
una matriz cuyo elemento ![]() vale 1, y con todos los demás elementos 0
vale 1, y con todos los demás elementos 0
Supongamos que tenemos ![]() distintas matrices tales que
distintas matrices tales que ![]() Entonces:
Entonces:
![]()
Por tanto: ![]() . Esto da una contradicción, así que hemos probado que C es única.
. Esto da una contradicción, así que hemos probado que C es única.
ii) C existe:
Sea![]() , con
, con ![]() . Como
. Como ![]() es lineal:
es lineal:
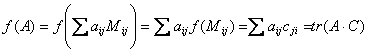
b) Sabemos que ![]() . Además, tenemos que
. Además, tenemos que
![]() . Entonces:
. Entonces:
![]() , por lo que podemos concluir que:
, por lo que podemos concluir que:
![]() , si
, si ![]() , y
, y ![]() si
si ![]() , luego
, luego ![]() y
y ![]() .
.
Otra forma de acabar: Como ![]() y para toda
y para toda ![]() , tomando
, tomando ![]() tenemos que
tenemos que
![]() , para todo
, para todo ![]() , luego los elementos de la diagonal de
, luego los elementos de la diagonal de ![]() son iguales. Por otro lado, tomando
son iguales. Por otro lado, tomando ![]() , tenemos que
, tenemos que
![]() , para todo
, para todo ![]() , luego los elementos de fuera de la diagonal principal son 0 y
, luego los elementos de fuera de la diagonal principal son 0 y ![]()
a) Sea ![]() una función continua. Decimos que
una función continua. Decimos que ![]() “cruza el eje” en
“cruza el eje” en ![]() si
si ![]() y en cualquier entorno de
y en cualquier entorno de ![]() existen
existen ![]() con
con ![]() .
.
Da un ejemplo de una función continua que “cruce el eje” infinitas veces.
(1997-Segundo día, Problema 6)
Solución
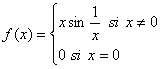
![]() es continua ya que
es continua ya que ![]() es continua en (0,1] y
es continua en (0,1] y
![]() ya que
ya que ![]() está acotada, y es fácil ver que cruza el eje infinitas veces, cada vez que
está acotada, y es fácil ver que cruza el eje infinitas veces, cada vez que ![]() , con
, con ![]() : Si
: Si ![]() , se cumple que
, se cumple que ![]() . Además, para los
. Además, para los ![]() tales que
tales que ![]() para algún
para algún ![]() , es decir, los
, es decir, los ![]() tales que
tales que 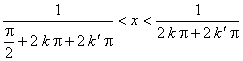 , se cumple que
, se cumple que ![]() , acercándose esos intervalos a
, acercándose esos intervalos a ![]() cuando
cuando ![]() tiende a infinito. Por otro lado, para los
tiende a infinito. Por otro lado, para los ![]() tales que
tales que ![]() para algún
para algún ![]() , es decir, los
, es decir, los ![]() tales que
tales que 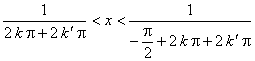 , se cumple que
, se cumple que ![]() , acercándose también esos intervalos a
, acercándose también esos intervalos a ![]() cuando
cuando ![]() tiende a infinito. Por tanto, en cualquier entorno de
tiende a infinito. Por tanto, en cualquier entorno de ![]() habrá puntos en los que la función es positiva y otros en los que es negativa, como queríamos.
habrá puntos en los que la función es positiva y otros en los que es negativa, como queríamos.
La función ![]() es dos veces diferenciable con continuidad y satisface que
es dos veces diferenciable con continuidad y satisface que ![]() . Prueba que existe un número real
. Prueba que existe un número real ![]() para el que
para el que ![]()
(1998-Primer día, Problema 4)
Solución
Sea ![]() . Como
. Como ![]() es dos veces diferenciable con continuidad,
es dos veces diferenciable con continuidad, ![]() es continua.
es continua.
En [0,1] la función ![]() alcanza un máximo y un mínimo.
alcanza un máximo y un mínimo.
Sea ![]() el punto donde se alcanza el máximo. Entonces si
el punto donde se alcanza el máximo. Entonces si ![]() , se cumple que
, se cumple que ![]() . (Cabría la posibilidad también de que
. (Cabría la posibilidad también de que![]() , pero en ese caso
, pero en ese caso ![]() , como queríamos)
, como queríamos)
Sea ![]() un punto donde se alcanza el mínimo. Entonces si
un punto donde se alcanza el mínimo. Entonces si ![]() , se cumple que
, se cumple que ![]() . (Cabe la posibilidad también de que
. (Cabe la posibilidad también de que ![]() , pero en ese caso
, pero en ese caso ![]() , como queríamos)
, como queríamos)
Como dijimos antes, g(x) es una función continua en [0,1], y g(x)<![]() . Si aplicamos el teorema de Bolzano, podemos asegurar que
. Si aplicamos el teorema de Bolzano, podemos asegurar que ![]() existe.
existe.
Notas:
1) No se han considerado los casos en que el máximo se alcanza en 0 ó el mínimo en 1. En esos casos es importante la condición de los valores de ![]() en los extremos, ya que, si quitamos por ejemplo la condición
en los extremos, ya que, si quitamos por ejemplo la condición ![]() , puede haber contraejemplos, como la función
, puede haber contraejemplos, como la función ![]() , que tiene el máximo en
, que tiene el máximo en ![]() , el mínimo en
, el mínimo en ![]() , cumple las otras dos condiciones
, cumple las otras dos condiciones ![]() ,
, ![]() , pero
, pero
![]() . Habrá que ver entonces cuando no hay máximo ó mínimo relativo dentro del intervalo si también se cumple
. Habrá que ver entonces cuando no hay máximo ó mínimo relativo dentro del intervalo si también se cumple ![]() cuando se dan las condiciones:
cuando se dan las condiciones:
![]()
2) El problema propuesto en ![]() fuera una función continua, sólo que existiera.
fuera una función continua, sólo que existiera.
Sea P un polinomio de grado n que tiene sólo raíces reales y coeficientes reales.
a) Prueba que para todo real x, se tiene la siguiente desigualdad:
![]()
b) Halla los casos en los que se alcanza la igualdad.
(1998-Primer día, Problema 5)
Solución
Sea ![]() . Entonces
. Entonces ![]() será
será
![]() , y
, y ![]() es
es
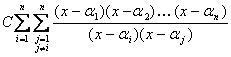 . Entonces la desigualdad se puede escribir como:
. Entonces la desigualdad se puede escribir como:
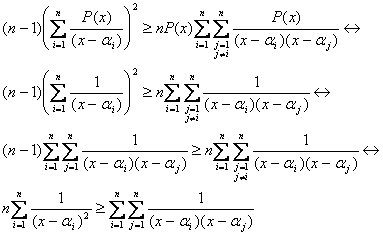
Ahora tenemos dos secuencias 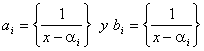 , así que si aplicamos la desigualdad de Chebishev obtenemos:
, así que si aplicamos la desigualdad de Chebishev obtenemos:
![]() , como queríamos.
, como queríamos.
La igualdad se alcanza si y sólo si ![]() , esto es si:
, esto es si:
![]() ,
, ![]() .
.
Nota:
La desigualdad de Chebishev es una consecuencia inmediata de la desigualdad de Reagrupamiento
Sea ![]() una función continua con la propiedad de que para todo x e y en el intervalo,
una función continua con la propiedad de que para todo x e y en el intervalo,
![]()
a) Demuestra que ![]()
b) Encuentra una función que satisfaga la condición para la que se alcance la igualdad.
(1998-Primer día, Problema 6)
Solución del apartado b)
La función ![]() ,
, ![]() , efectivamente cumple las condiciones: si consideramos la función
, efectivamente cumple las condiciones: si consideramos la función ![]() , con
, con ![]() , tenemos que para cualquier
, tenemos que para cualquier ![]() el máximo absoluto de esa función es 1, ya que
el máximo absoluto de esa función es 1, ya que ![]() , teniéndose que:
, teniéndose que:
![]() ,
, ![]() ,
, ![]()
Se cumple además que ![]() , al ser
, al ser ![]() el área de un cuarto de círculo de radio 1
el área de un cuarto de círculo de radio 1